A mecânica da fratura como base do projeto tolerante ao dano
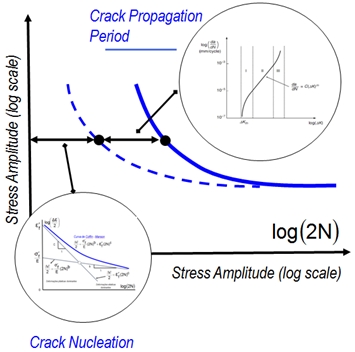
Não é tarefa fácil discorrer sobre a mecânica da fratura em cinco ou seis linhas, e menos ainda sobre todo o aparato numérico necessário para a correta descrição do fenômeno. Grande ainda é o número dos que confundem o fenômeno da fadiga com o da mecânica da fratura e menor ainda é o grupo daqueles que sabem que a estratégia de projeto é bem distinta quando se projeta para evitar a fadiga (nucleação de uma trinca) ou quando a intenção é que o projeto seja tolerante ao dano. E é justamente este tipo de equívoco que causou o naufrágio de centenas de “Liberty Ships” no período da segunda grande guerra e ainda hoje faz suas vítimas nas indústrias mecânica, civil e aeronáutica. O que normalmente os engenheiros veem é a fratura final (o componente quebrado, digamos assim) e o que eles normalmente ignoram é que pode ter havido uma fase relativamente significativa de propagação de uma trinca que teve origem no fenômeno da fadiga. E é justamente nesta propagação que o presente artigo está interessado. O gráfico abaixo ajuda a entender melhor.
A linha pontilhada marca a nucleação de uma trinca. Fica fácil observar que, para alternadas maiores e baixo número de ciclos, é relevante o estudo da mecânica da fratura e, ainda no mesmo raciocínio, para alto número de ciclos, a distância que separa a nucleação da total fratura é praticamente inexistente e, assim, nestas circunstâncias, o projeto deve reunir esforços no sentido de evitar completamente o surgimento de uma trinca. Em outras palavras, podemos desprezar a mecânica da fratura. No pioneiro trabalho de A. A. Griffith (1920), o conceito de taxa de liberação da energia de deformação levou ao conceito de fator de intensidade de tensões K, que em linhas gerais pode ser definido como na equação abaixo: 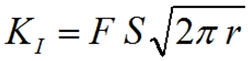 Há uma dependência básica com relação à tensão aplicada e ao fator geométrico F, que é o item mais delicado da metodologia proposta. Esse fator K, vale dizer, é um parâmetro muito importante para a correta compreensão da “severidade”, digamos assim, de uma determinada trinca instalada. Este valor pode ser diretamente comparado com os limites de tenacidade à fratura dos materiais empregados. Para os metais, geralmente, estes valores se encontram dentro do intervalo que vai de 20 a 200 MPa.m1/2. Com o aumento do limite de ruptura, dentro de uma determinada classe de materiais, nota-se ainda que há um decréscimo nos valores de (KIC), seguindo a mesma tendência da ductilidade do material. A fim de calcular os valores de K ao longo de uma trinca em um determinado componente, utilizaremos o conceito da integral J, implementado já na versão 11 do ANSYS, podendo ser acessado através do comando CINT, que iremos detalhar a seguir. Basicamente, a integral J é a extensão do conceito de Griffith para os casos onde há não-linearidade elástica envolvida, como mostra o esboço da figura 2.
Há uma dependência básica com relação à tensão aplicada e ao fator geométrico F, que é o item mais delicado da metodologia proposta. Esse fator K, vale dizer, é um parâmetro muito importante para a correta compreensão da “severidade”, digamos assim, de uma determinada trinca instalada. Este valor pode ser diretamente comparado com os limites de tenacidade à fratura dos materiais empregados. Para os metais, geralmente, estes valores se encontram dentro do intervalo que vai de 20 a 200 MPa.m1/2. Com o aumento do limite de ruptura, dentro de uma determinada classe de materiais, nota-se ainda que há um decréscimo nos valores de (KIC), seguindo a mesma tendência da ductilidade do material. A fim de calcular os valores de K ao longo de uma trinca em um determinado componente, utilizaremos o conceito da integral J, implementado já na versão 11 do ANSYS, podendo ser acessado através do comando CINT, que iremos detalhar a seguir. Basicamente, a integral J é a extensão do conceito de Griffith para os casos onde há não-linearidade elástica envolvida, como mostra o esboço da figura 2.
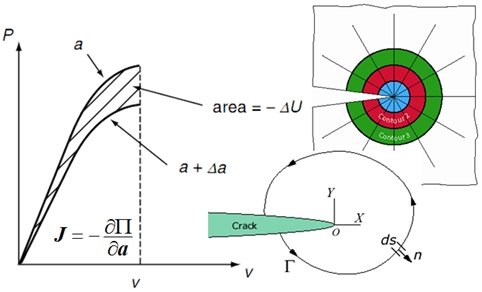
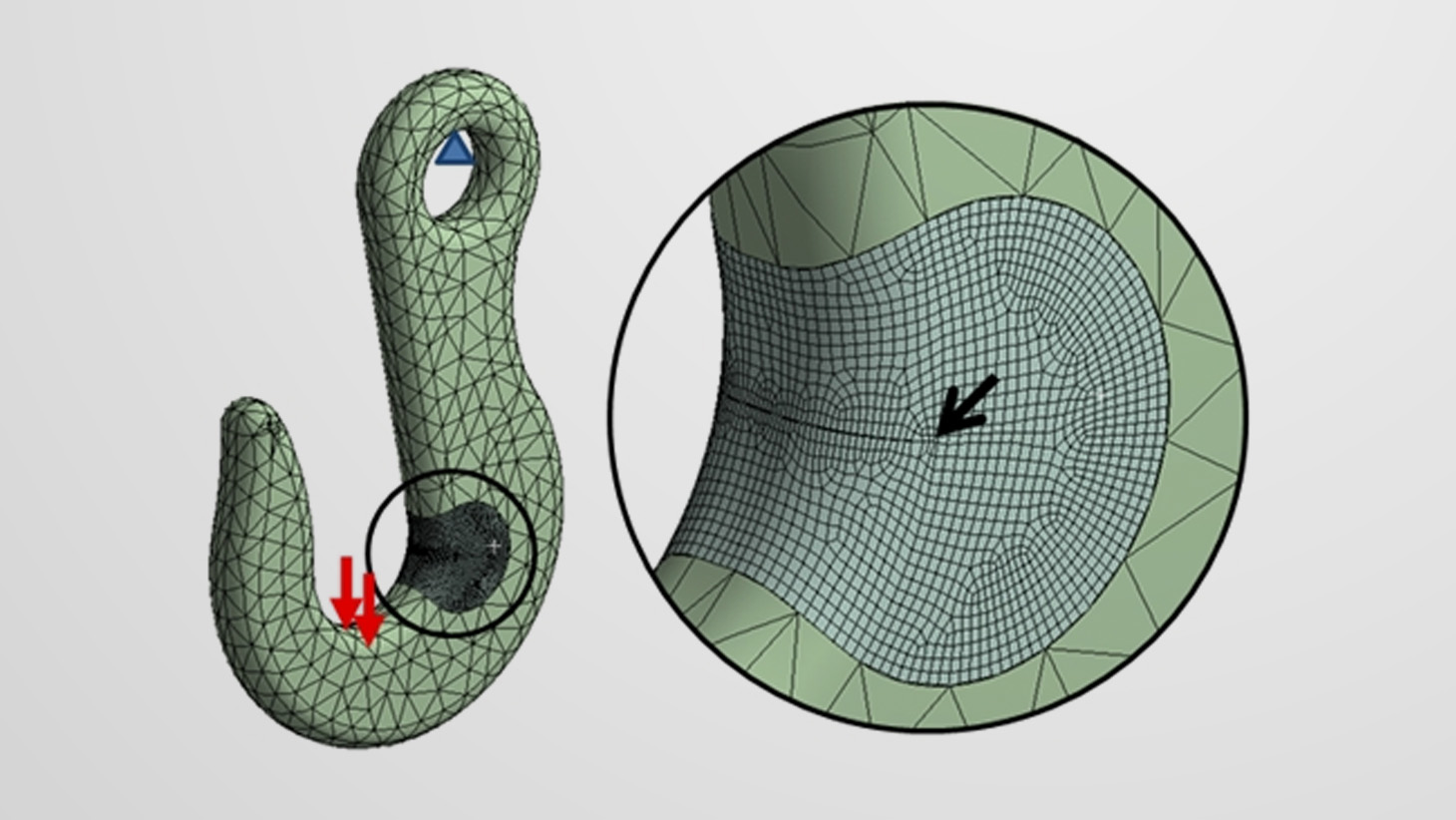
Figura 2 – Modelo de gancho com fratura.
Considere agora o modelo apresentado na figura 3, no qual introduzimos uma trinca, tomando o cuidado de gerar uma malha controlada (hexadominante) na região que a envolve. O tipo de elemento empregado é tão importante quanto a densidade elementar, para a fiel representação do campo de tensões, cujo gradiente é elevado por natureza.
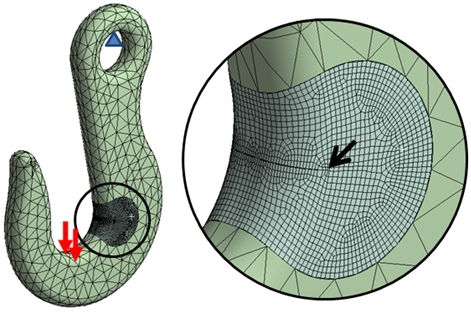
Figura 3 – Modelo de gancho com fratura.
Se os valores de tensão obtidos forem comparados diretamente, vale dizer, com os limites de escoamento e ruptura do material, corremos o sério risco de superestimar a severidade do carregamento imposto, em função da singularidade matemática envolvida.
O primeiro passo, no Workbench, é a definição de um sistema de coordenadas local numa das faces da trinca, o que na figura 4 é mostrado como sistema (Rsys=17). É preciso ainda definir um grupo contendo os nós que pertencem à aresta da trinca a ser estudada. Ainda na figura 4 tem-se a sequência com os seis comandos necessários para o cálculo da integral J. O argumento (NEW) define uma trinca a ser calculada, relativa ao componente “ArestaTrinca” (CTNC), que nada mais é que um conjunto de nós. (NCONTOUR) solicita que o cálculo da integral J seja realizado em uma determinada quantidade de contornos. E o argumento (NORM) faz a escolha do vetor e do sistema de coordenadas relacionados à superfície livre da trinca.
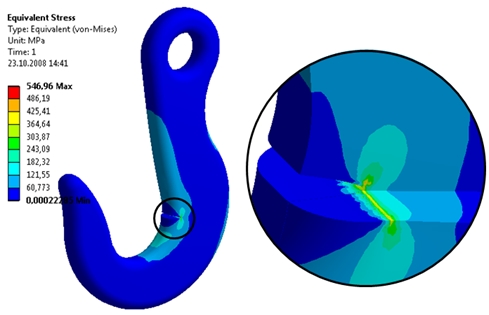
Figura 5 – Gradiente das tensões equivalentes de Von Mises.
A julgar pelos valores das tensões equivalentes de Von Mises (figura 5), por exemplo, um material como o aço MAN-TEN, com limite de ruptura na casa de 450MPa, já estaria seriamente comprometido. Para este mesmo material, contudo, o (KIC) é cerca de 6320 MPa.(mm1/2). Também na figura 6 temos uma idéia do forte gradiente em torno da trinca, com altíssimas tensões de natureza trativa, cuja distribuição é extremamente dependente da qualidade da malha utilizada.
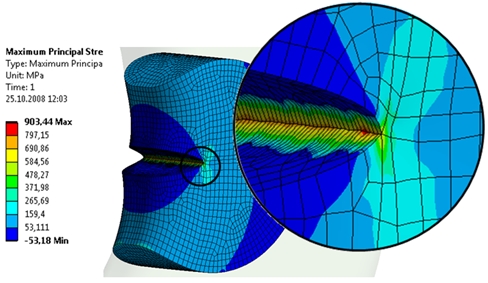
Figura 6 – Gradiente das tensões máximas principais
![]()
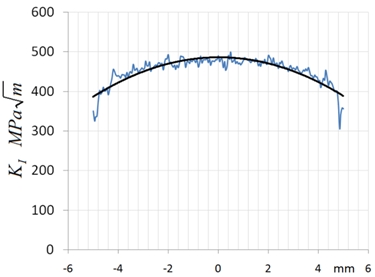
Os valores de KI , para o componente acima, está distribuído, ao longo da trinca existente, conforme a curva da figura 7.
A oscilação observada é numérica, antes de mais nada, e está relacionada à qualidade da discretização e dos elementos utilizados para representar a região de dominância K.
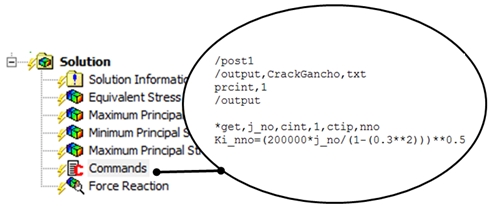
Figura 8 – Estrutura dos comandos necessários.
Na figura 8 são apresentados os mínimos comandos necessários para acessar o valor da integral J e convertê-lo ao valor de K para um determinado nó pertinente à fratura estudada. O comando (/OUTPUT,CrackGancho,txt) direciona a saída de texto para o arquivo (CrackGancho.txt). O comando (PRCINT,1), na figura 9, diz ao ANSYS que escreva o valor da integral J correspondente à cada nó pertinente à (ArestaTrinca) no arquivo (CrackGancho.txt).
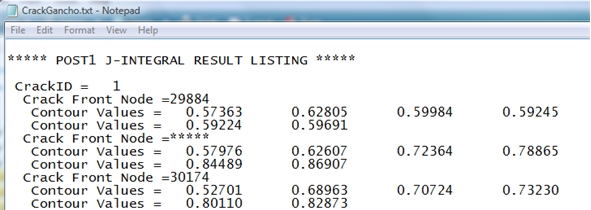
Figura 9 – Saída de dados (Integral J) do comando (PRCINT).
O acesso aos valores da integral J também podem ser feitos através do comando (*GET). No exemplo citado na figura 8, é solicitado ao ANSYS que escreva o valor da integral J da trinca de número (1) do nó (NNO) na variável (J_NO). O restante é apenas parte da sintaxe do comando. Ainda na figura 8, a equação disponível é responsável por converter os valores da integral J para o valor de KI. Basicamente:  Estes comandos devem ser repetidos para cada um dos nós do componente (Aresta Trinca), através, por exemplo, da utilização dos comandos de loop (*DO / *ENDDO). Aqui recomendamos que o usuário familiarize-se um pouco mais com a estrutura da linguagem APDL (ANSYS Programming Design Language). Com os recursos disponíveis no ANSYS é possível, portanto, julgar a severidade de uma trinca ou um defeito, através da comparação dos valores de KI com os valores da tenacidade à fratura do material utilizado na fabricação do componente. Outra pergunta ainda a ser respondida, dentro do mesmo tema da “mecânica da fratura”, seria a de quantos ciclos seriam necessários para levar a trinca existente até o estado de completa fratura do componente, ou, em outras palavras, chegar até o ponto em que a trinca possui o chamado “tamanho crítico”, ponto no qual os valores de KI para o material atingiriam o valor necessário para fratura frágil (figura 10).
Estes comandos devem ser repetidos para cada um dos nós do componente (Aresta Trinca), através, por exemplo, da utilização dos comandos de loop (*DO / *ENDDO). Aqui recomendamos que o usuário familiarize-se um pouco mais com a estrutura da linguagem APDL (ANSYS Programming Design Language). Com os recursos disponíveis no ANSYS é possível, portanto, julgar a severidade de uma trinca ou um defeito, através da comparação dos valores de KI com os valores da tenacidade à fratura do material utilizado na fabricação do componente. Outra pergunta ainda a ser respondida, dentro do mesmo tema da “mecânica da fratura”, seria a de quantos ciclos seriam necessários para levar a trinca existente até o estado de completa fratura do componente, ou, em outras palavras, chegar até o ponto em que a trinca possui o chamado “tamanho crítico”, ponto no qual os valores de KI para o material atingiriam o valor necessário para fratura frágil (figura 10).
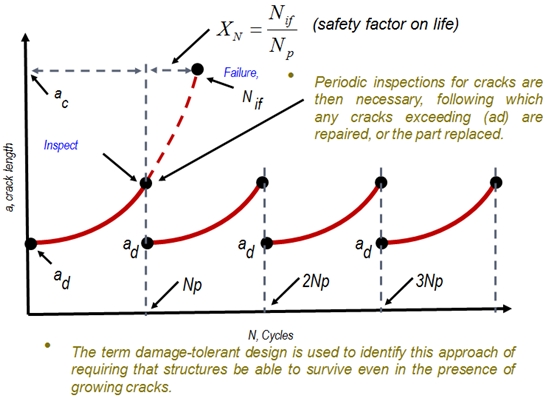
Figura 10 – Conceito de Projeto Tolerante ao Dano empregado para determinação dos intervalos de manutenção.
Para responder a esta pergunta é necessário o estudo da propagação da trinca, o que envolve uma nova teoria e metodologias, que o ANSYS em bem pouco tempo será capaz de lidar de maneira automática. A figura 11 representa a curva de propagação de um material qualquer. Número de ciclos em função da alternada dos fatores de concentração de tensão (DK). Os dois “thresholds” são os dois limites abaixo ou acima dos quais a propagação não ocorre, ou ocorre de maneira frágil e instantânea. A lei de Paris, ainda no mesmo gráfico esboçada, é válida, então, na segunda região.
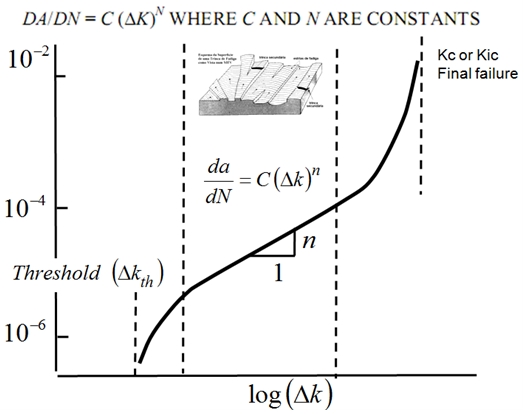
Figura 11 – Lei de propagação de Paris.
Como desenvolvimentos futuros, a ANSYS nos apresenta a lista que se segue: DOWNLOAD 1. T-stress calculation 2. CINT enhancement a. Surface element support b. Inertial loading c. Initial state (initial strain, stress, …) d. C* for creep material 3. Crack growth simulation a. Mesh morphing b. Remeshing 4. Workbench meshing 5. Composite fracture E, assim, podemos finalizar dizendo que a ANSYS está evoluindo de maneira consistentemente sólida, com a intenção de fornecer soluções na mesma medida profundas, em termos teóricos e técnicos, e abrangentes, de forma a garantir que os usuários tenham a melhor solução totalmente integrada do mercado.
Por Giovanni Moraes Teixeira, Antônio Carlo Guimarães, Ivan Thesi Ragusoff, Fernando Amaral Polastro, ESSS